Aho-corasick (아호코라식)
코드
#include <stdio.h>
#include <memory.h>
#include <queue>
using namespace std;
struct Trie
{
Trie *go[26], *fail;
bool finish;
Trie() : finish(false), fail(NULL) {
memset(go, 0, sizeof(go));
}
~Trie() {
for (int i = 0; i < 26; i++)
if (go[i])
delete go[i];
}
void insert(const char *key) {
if (*key == '\0')
finish = true;
else {
int curr = *key - 'a';
if (go[curr] == NULL)
go[curr] = new Trie;
go[curr]->insert(key + 1);
}
}
};
void make_aho(Trie *root) {
queue<Trie*> q;
q.push(root);
while (!q.empty()) {
Trie *current = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
Trie *next = current->go[i];
if (!next) continue;
if (current == root) next->fail = root;
else {
Trie *dest = current->fail;
while (dest != root && !dest->go[i])
dest = dest->fail;
if (dest->go[i])
dest = dest->go[i];
next->fail = dest;
}
if (next->fail->finish)
next->finish = next->fail->finish;
q.push(next);
}
}
}
bool find_aho(Trie *root, char *s) {
int i;
Trie *current = root;
for (i = 0; s[i]; i++) {
int next = s[i] - 'a';
while (current != root && !current->go[next])
current = current->fail;
if (current->go[next])
current = current->go[next];
if (current->finish)
return true;
}
return false;
}
int main()
{
int n, q, i;
char s[10001];
Trie *root = new Trie;
scanf("%d", &n);
while (n--) {
scanf("%s", s);
root->insert(s);
}
make_aho(root);
scanf("%d", &q);
while (q--) {
scanf("%s", s);
printf("%s\n", find_aho(root, s) ? "YES" : "NO");
}
return 0;
}
문자열 집합 판별 - https://www.acmicpc.net/problem/9250
정리
- 일대다 패턴매칭 알고리즘, KMP의 확장형 알고리즘이다. O(N+m1+m2+...+mk) 시간복잡도를 가진다.
- 아호코라식은 기본적으로 트라이이다.
- 아호코라식은 다음과 같은 함수로 구성된다.
- go 함수 : 다음 state 를 정의하는 함수
- output 함수 : output(finish) 노드를 지날 때 단어의 목록을 내뱉는 함수
- fail 함수 : 알고리즘을 진행하면서 갈곳이 없어지면, 단순히 시작 지점이 아니라 다른 곳으로 보내는 함수 (kmp 의 실패함수와 비슷하다)
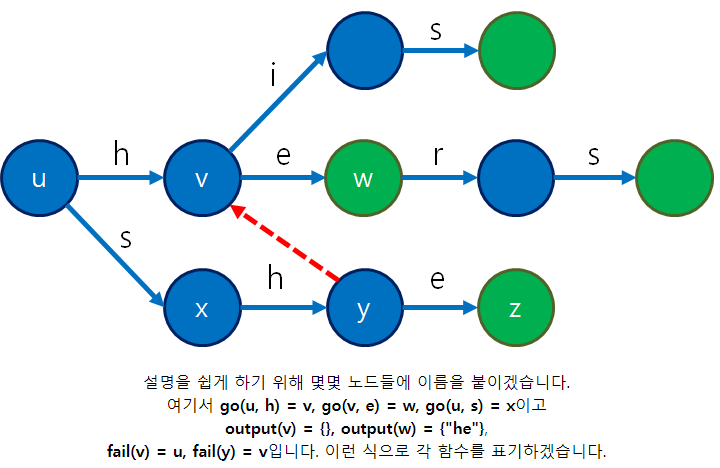
- 함수는 아래의 그림 처럼 사용된다
실패함수를 찾는 방법 - fail(y) = v, fail(z) = w 인 이유
- 최근 입력된 문자열(접미사)이, 트라이의 접두사와 일치한다.
- sh 를 검색했을 때, 트라이의 처음부터 h가 검색되었다고 생각할 수 있다.
- 마찬가지로 she 가 검색되었을 때, 트라이의 처음부터 he가 검색되었다고 생각할 수 있다.
즉 fail(x) = y 면, x의 접미사 중 하나가 반드시 y이다. (단, 접미사가 x는 아니다), 또한, y는 가능한 한 가장 긴 접미사이다. -> 따라서 fail 함수의 결과는 깊이가 줄어든다. (|fail(x)| < |x|)
Q1. 만약 같은 스펠링을 가진 노드가 엄청 많다면?
- 이 경우는 KMP에서 fail 이 여러번 이동하는 것과 같은 경우이다.
- fail 함수는 루트를 제외하고 반드시 자신보다 깊이가 작은 노드를 가리킨다.
- fail(x) = y 일 때, y는 x의 접미사(x는 아니다) + y는 가능한 한 가장 긴 접미사 로 결정한다.
Q2. {"adada", "ac"} 일때 "adadac" 를 찾는다면, ac 를 어떻게 찾을 수 있을까?
- adada + c 를 할 때, 실패하므로
- 가장 긴 접미사 ada 로 간다. 하지만 ada + c 도 실패하므로
- 가장 긴 접미사 a로 간다. a + c 는 성공이므로 output 함수를 호출한다.
결론. fail 함수가 주어졌을 때 매커니즘은 다음과 같다
- 현재 state x, 인풋 c에 대해 go(x, c)가 있으면 거기로 이동한다
- 만약 없다면 fail(x)로 이동한 후 1로 돌아간다. (단, 루트면 아무것도 하지 않는다.)
fail 함수를 만드는 방법
- fail 은 트라이상에 존재하는 x의 가장 긴 접미사 노드이며, x는 아니다.
- BFS 를 통해 깊이가 작은 노드부터 방문해가며 fail 함수를 DP를 적용하듯이 결정한다.
- 트라이상의 문자열 x, yx가 있을 때, fail(yx) = x 라 하자, 똑같은 문자열 z를 더 이어 붙이면 fail(yxz) = xz 이다 오토마타상에서 fail을 간선으로 나타내면 평행선을 그리게 된다.
- 이러한 구조로 인하여, 문자열 p가 있을 때 문자 x를 이어 붙이면
- fail(px) = go(fail(p), x) -> 바텀업 DP 이다.
- fail(x) = y 일 때, output(y) 는 output(x)에 포함된다.
구현은 다음과 같다
트라이를 만든다.
트라이에 패턴의 원소를 모두 집어 넣는다.
fail 함수를 만든다 (BFS를 통해 트라이 노드를 방문) (이 과정에서 current->go[i] 의 fail 함수를 결정한다)
BFS 시작하기 전에, root 를 먼저 queue 에 넣는다.
root->fail = root;
BFS (큐가 빌때까지 반복)
큐에서 현재 노드를 가져온다 (current = Q.front())
input 에 대해 각각 반복을 돌린다 (a-z)
next 가 없다면 continue
current == root 이면, next->fail = root; 이다. (당연하다)
current != root 이면, (dest=current->fail, dest 가 root 이거나, go[i] 가 있을때까지 반복한다)
dest = current->fail;
while (current != root && !dest->go[i]) dest = dest->fail; (실패함수를 계속 찾음)
if (dest->go[i]) dest = dest->go[i]; (dest->go[i] 가 있으면, 그곳이 실패함수의 목적지)
next->fail = dest; (current->go[i] 의 fail 함수를 목적지로 지정한다)
next->fail->output == true 이면, next->output = true 이다.
각 문자열을 받아서 문제를 푼다.
current = root, 트라이의 root에서 시작한다
문자열의 문자를 하나씩 읽으며 처리한다
(while)루트가 아니고 다음으로 갈수 없다면, 실패함수로 이동한다.
go 함수가 존재하면 이동한다.
현재 노드에 output 이 있다면 (finish), 찾은 것이다.
관련 문제
- 9250 : 문자열 집합 판별
- 10256 : 돌연변이 ★
- 5735 : Emoticons ★
- 6300 : Word Puzzles