Merge Sort Tree

세그먼트 트리인데, 완전이진트리에서 각각 정렬된 벡터(vector<int>)를 가진다. (build : O(nlogn))

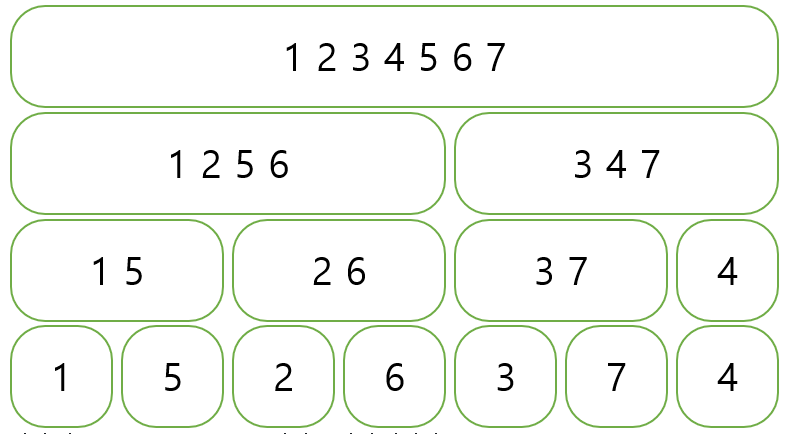
query 과정에서 merge 를 할때 left, right 에 대한 순서가 보장된다.

i~j 구간에 k 번째 수를 찾는다면, binary search를 통해 x 값을 찾고(logn),

upper_bound 로 x 를 찾았을 때 인덱스 값을 모두 더하여 찾는다.(log^n) (query : O(log^3n))

값 갱신이 아닌 query 사용이 잦은 문제에 활용될 가능성이 높다. (1회 build 이후, 계속 query)

코드

#include <stdio.h>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> tre[100003 << 2];

void update(int l, int r, int node, int idx, int val)
{
    if (idx < l || r < idx)
        return;
    tre[node].push_back(val);
    if (l < r) {
        int mid = (l + r) / 2;
        update(l, mid, node * 2, idx, val);
        update(mid + 1, r, node * 2 + 1, idx, val);
    }
}

int query(int l, int r, int node, int start, int end, int x)
{
    if (end < l || r < start)
        return 0;
    if (start <= l && r <= end)
        return upper_bound(tre[node].begin(), tre[node].end(), x) - tre[node].begin();
    int mid = (l + r) / 2;
    return query(l, mid, node * 2, start, end, x) + query(mid + 1, r, node * 2 + 1, start, end, x);
}

int main()
{
    int n, m, i, j, k;

    scanf("%d%d", &n, &m);
    for (i = 1; i <= n; i++) {
        scanf("%d", &j);
        update(1, n, 1, i, j);
    }

    for (i = 1; i <= n*4; i++)
        sort(tre[i].begin(), tre[i].end());

    while (m--) {
        scanf("%d%d%d", &i, &j, &k);
        int l = -1e9, r = 1e9, mid, ans = r;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (query(1, n, 1, i, j, mid) >= k)
                ans = mid, r = mid - 1;
            else
                l = mid + 1;
        }
        printf("%d\n", ans);
    }

    return 0;
}

정리

관련문제

https://www.acmicpc.net/problem/7469

참고

https://justicehui.github.io/2018/11/24/BOJ7469.html